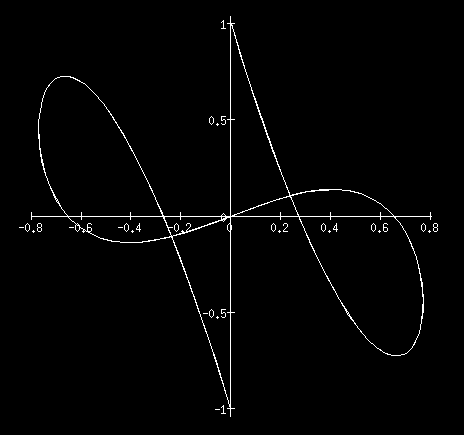ThinkQuest Project |
This site, part of the ThinkQuest project, considers whether
Maurits Corneille Escher (1898-1972) was an artist or
a mathematician. Ample illustrations and discussion are provided.
Official M. C. Escher Web Site |
This is the official M. C. Escher Web site. It contains art, a brief
biography, news, a bibliography, and other links. It is maintained by
the M. C. Escher Foundation. Escher spent a considerable amount
of time at the Alhambra in Granada, Spain developing his
artistic philosophy.

Mathematical Analysis of Escher's Work |
This site gives a mathematical analysis of Escher's work, particularly
of his concept of dimensionality. Some of his woodcuts are related
to ideas of Poincaré and Möbius.

Catalog of M. C. Escher's Graphic Works |
This site gives a catalog of some of M. C. Escher's graphic works,
compiled by Zvi Har'El.

Graphs of Curves |
This is a gallery of graphs of curves compiled by the University of Pennsylvania
Physics Department.
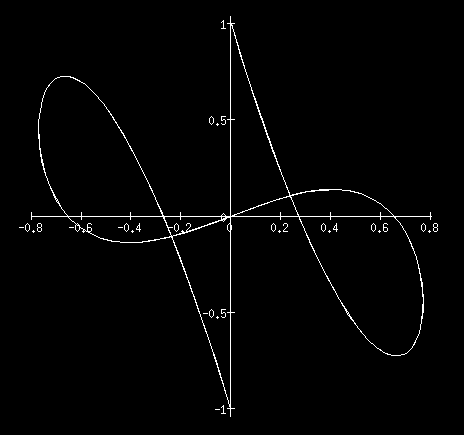
Sculpture by George W. Hart |
This is a gallery of sculpture by George W. Hart. In his own words,
"As a sculptor of constructive geometric forms, my work deals with patterns
and relationships derived from classical ideals of balance and symmetry.
Mathematical yet organic, these abstract forms invite the viewer to partake
of the geometric aesthetic. I use a variety of media, including paper,
wood, plastic, metal, and assemblages of common household objects."

Links Between Geometry and Physics |
This site in Germany explores links between geometry and physics.
It has hot buttons for other geometry pages.

Teaching Children about Geometry |
This site explores teaching children about geometry.
There are discussions of grids, graphs, and patterns,
of coloring polygons, and of many other lively topics.
Mathematical Theory of Knots |
This is a page on the mathematical theory of knots.
Major sections are on Knot Tying, Knot Theory, and Knot Art. But knot lovers
will understand that these distinctions are artificial. For example, a good practical
knot is both a nugget of hard-won technology and a thing of beauty.
Decorative knotting can be useful, and in any case requires uncommon
dexterity and practical tying ability. Software developed to help mathematical
knot theorists has produced some of the most beautiful knot images ever seen.

Mathematical Artistic Work of Koos Verhoeff |
This page features the mathematical artistic work of
Koos Verhoeff. Born in Holland in 1927, Koos Verhoeff
approaches his artistic designwork with a background in
mathematics and computer science. After studying at the
Universities of Leiden and Amsterdam, Koos went on to work at
the Mathematical Center in Amsterdam (1952-1957) and the Delft
University of Technology. During that time the Dutch artist
M.C. Escher frequented the Mathematical Center to research
many of the mathematical principles he applied to his work.
Inspired by Escher, Verhoeff became interested in the great
potential for mathematical applications to artwork.

Robbert Dijkgraaf, Mathematician/Physicist and Sculptor |
Robbert Dijkgraaf (1960) is since 2005 University Professor at the University of
Amsterdam, where from 1992 he held the chair of Mathematical Physics. He studied
theoretical physics and mathematics in Utrecht, where (after an interlude studying
painting at the Gerrit Rietveld Academie) he obtained his Ph.D. cum laude under
supervision of Gerard 't Hooft in 1989. Subsequently he held positions at Princeton
University and the Institute for Advanced Study. His research group works in string
theory, quantum gravity, and the interface of mathematics and particle physics. He manages
the FOM programs Mathematical Physics and String Theory and Quantum Gravity.
He is also interested in creating more public awareness of mathematics and science,
and bridging the gap with the arts and humanities.
Bonner Design Consultancy |
Jay Bonner is a specialist in the design of Islamic geometric patterns.
Some 25 years ago he rediscovered the lost techniques used by traditional
Muslim pattern designers. These techniques provide the means to recreate
even the most complex patterns used by Islamic cultures of the past, as
well as to create original Islamic geometric patterns that are wholly
in keeping with this great tradition.
Jay Bonnerís research in this field has lead to his
writing a book on this fascinating subject: Islamic Geometric Patterns:
Their Historical Development and Traditional Methods of Derivation.
This book is both an historical study, as well as a comprehensive exposition
of the traditional methods used in the creation of these complex
designs, with over 240 detailed illustrations.


Anatoly Fomenko, Mathematician and Artist |
Anatoly Fomenko is a distinguished mathematician whose
work has been in the subject area of global analysis, geometry,
and mechanics. His work has a dark, brooding quality. It is
geometrical, but it also has human depth.

Richard Termes, Artist |
Dick Termes is an internationally acclaimed artist. His work has been recognized from San Francisco to
Paris, France, from New York to Japan. Unlike any other painter; he paints on spheres which, when completed,
are known as Termespheres. Each sphere is a revolving three-dimensional space/time exploration of an entirely
closed universe. Visit the Gallery to experience Termespheres for yourself.